amep.spatialcor.rdf

amep.spatialcor.rdf(coords: ndarray, box_boundary: ndarray, other_coords: ndarray | None = None, nbins: int | None = None, rmax: float | None = None, mode: str = 'diff', chunksize: int | None = None, njobs: int = 1, pbc: bool = True, verbose: bool = False) → tuple[ndarray, ndarray]

Calculate the radial pair-distribution function for a single frame. Provides two modes: mode=’diff’ loops through all particles and calculates the distance to all others as simple difference of the position vectors and use=’kdtree’ uses the scipy.spatial.cKDtree to determine the distances between the particles. It depends on your hardware which option is the fastest. Using the ‘kdtree’ usually needs more memory but could be slightly faster than ‘diff’.

Notes

The radial pair-distribution function between two particle species i and j is defined by (see Refs. [1] [2])

\[\begin{split}g_{ij}(r) = \frac{1}{\rho_j N_i}\sum\limits_{k\in S_i} \sum\limits_{\substack{l\in S_j \\ l\neq k}} \left\langle\frac{\delta\left(r-\left|\vec{r}_k(t)-\vec{r}_l(t)\right|\right)}{4\pi r^2}\right\rangle_t\end{split}\]

For i=j we have

\[g(r) = \frac{1}{\rho N}\sum\limits_{k}\sum\limits_{l\neq k} \left\langle\frac{\delta\left(r-\left|\vec{r}_k(t)-\vec{r}_l(t)\right|\right)}{2\pi r}\right\rangle_t\]

References

[1]

Abraham, M. J., Hess, B., Spoel, D. van der, Lindahl, E., Apostolov, R., Berendsen, H. J. C., Buuren, A. van, Bjelkmar, P., Drunen, R. van, Feenstra, A., Fritsch, S., Groenhof, G., Junghans, C., Hub, J., Kasson, P., Kutzner, C., Lambeth, B., Larsson, P., Lemkul, J. A., … Maarten, W. (2018). GROMACS User Manual version 2018.3. 258. www.gromacs.org

[2]

Hecht, L., Horstmann, R., Liebchen, B., & Vogel, M. (2021). MD simulations of charged binary mixtures reveal a generic relation between high- and low-temperature behavior. The Journal of Chemical Physics, 154(2), 024501. https://doi.org/10.1063/5.0031417

Parameters:

• coords (np.ndarray of shape (N,3)) – Coordinates.

• box_boundary (np.ndarray of shape (3,2)) – Boundary of the simulation box in the form of np.array([[xmin, xmax], [ymin, ymax], [zmin, zmax]]).

• other_coords (np.ndarray or None, optional) – Coordinate frame of the other species to which the pair correlation is calculated. The default is None (uses coords).

• nbins (int or None, optional) – Number of distance bins. The default is None.

• rmax (float or None, optional) – Maximum distance to consider. The default is None.

• mode (str, optional) – Allows to choose the calculation method. Available modes are ‘diff’ and ‘kdtree’. The default is ‘diff’.

• chunksize (int or None, optional) – Divide calculation into chunks of this size. The default is None.

• njobs (int, optional) – Number of jobs for multiprocessing. The default is 1.

• pbc (boolean, optional) – If True, periodic boundary conditions are applied. The default is True.

Returns:

• gr (np.ndarray) – g(r) (1D array of floats)

• r (np.ndarray) – distances (1D array of floats)

Examples

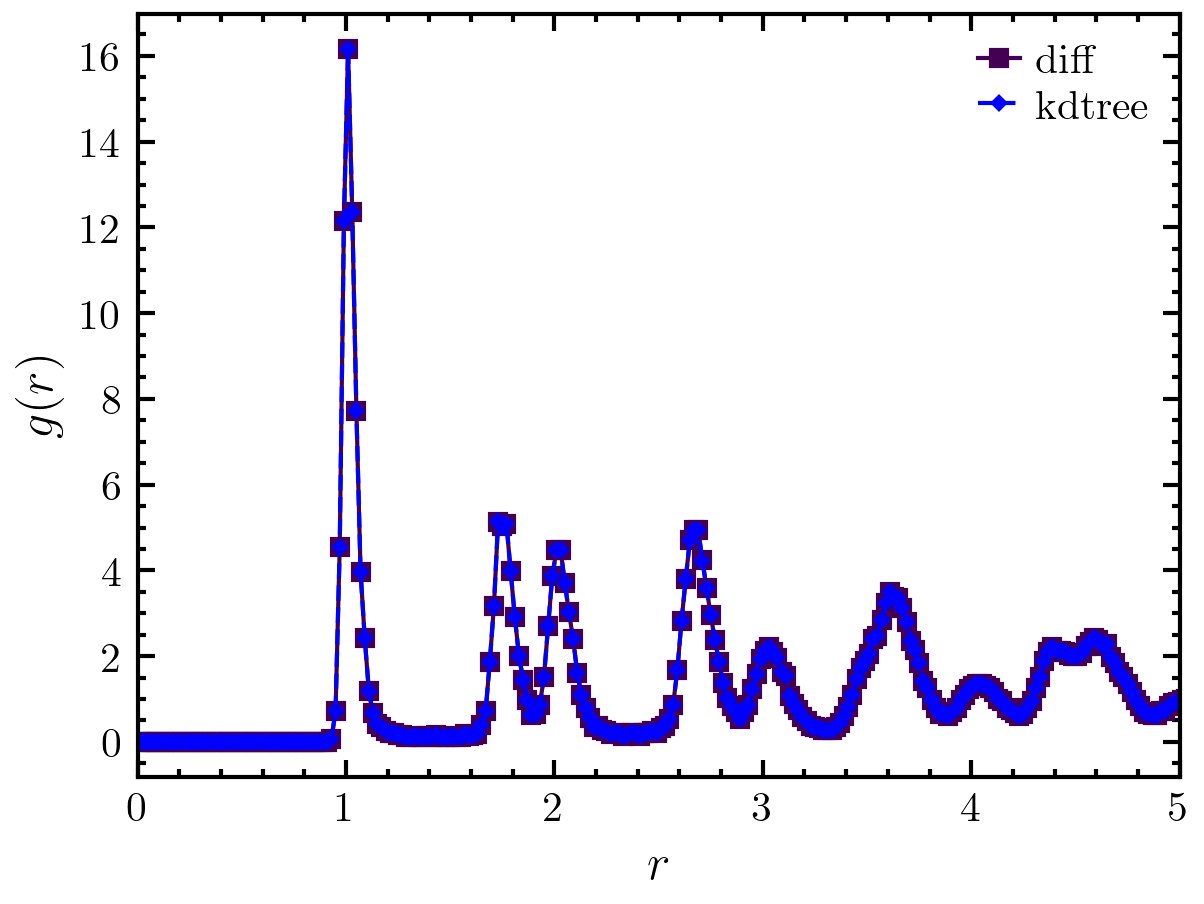
>>> import amep
>>> traj = amep.load.traj("../examples/data/lammps.h5amep")
>>> frame = traj[-1]
>>> gr1, r1 = amep.spatialcor.rdf(
...     frame.coords(), frame.box, mode='diff', rmax=10,
...     verbose=True, njobs=1, pbc=True
... )
>>> gr2, r2 = amep.spatialcor.rdf(
...     frame.coords(), frame.box, mode='kdtree', rmax=10,
...     verbose=True, njobs=1, pbc=True
... )
>>> fig, axs = amep.plot.new()
>>> axs.plot(r1, gr1, label='diff', markersize=4)
>>> axs.plot(r2, gr2, label='kdtree', ls='--', c='b')
>>> axs.legend()
>>> axs.set_xlabel(r'$r$')
>>> axs.set_ylabel(r'$g(r)$')
>>> axs.set_xlim(0,5)
>>> fig.savefig('./figures/spatialcor/spatialcor-rdf.png')
>>>