amep.spatialcor.pcf_angle

amep.spatialcor.pcf_angle(coords: ndarray, box_boundary: ndarray, other_coords: ndarray | None = None, ndbins: int | None = None, nabins: int | None = None, rmax: int | None = None, psi: ndarray | None = None, njobs: int = 1, pbc: bool = True, verbose: bool = False, chunksize: int | None = None) → tuple[ndarray, ndarray, ndarray]

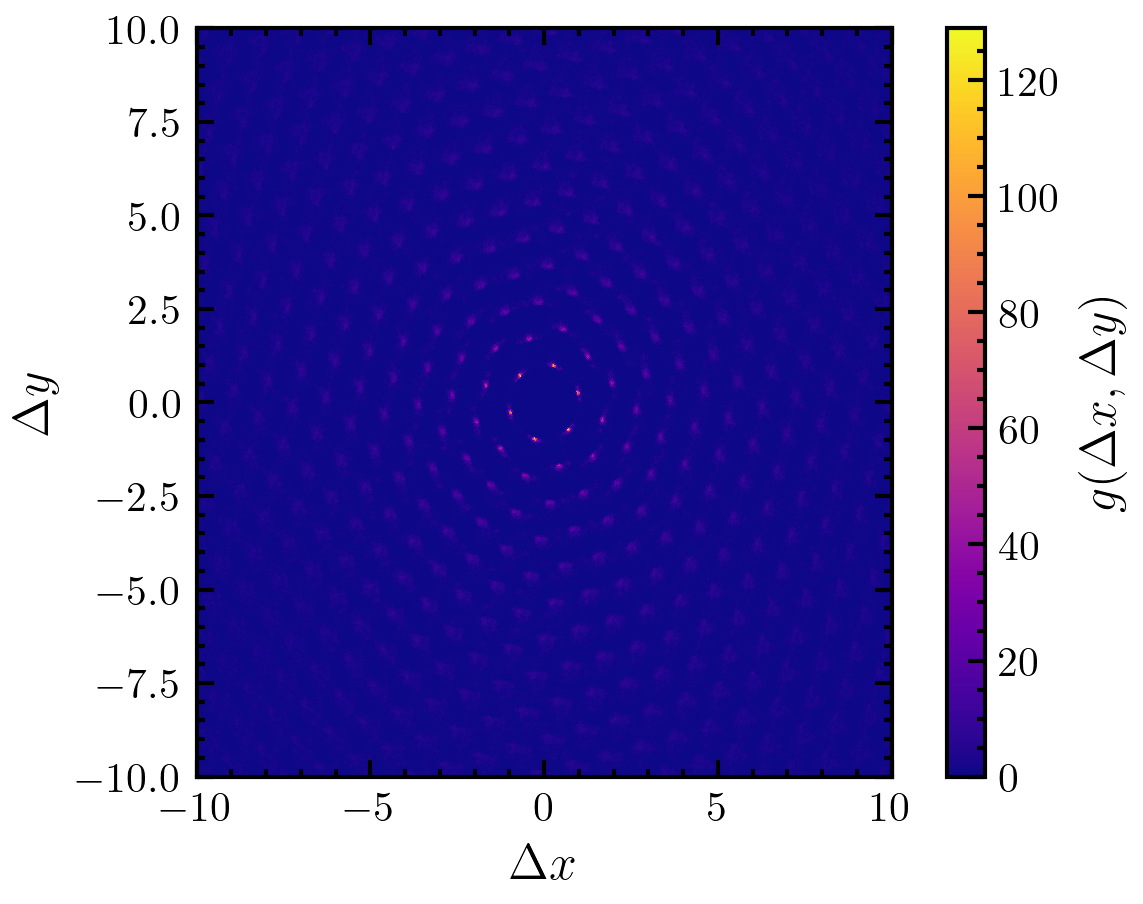
Calculate the angle dependent radial pair correlation function.

Do that by calculating histograms. To allow for averaging the result (either with respect to time or to make an ensemble average), the coordinates are rotated such that the mean orientation (given by the vector psi) points along the x axis (see Ref. [1] for details).

Notes

The angle-dependent pair correlation function is defined by (see Ref. [2])

\[g(r,\theta) = \frac{1}{\langle \rho\rangle_{local,\theta} N}\sum\limits_{i=1}^{N} \sum\limits_{j\neq i}^{N}\frac{\delta(r_{ij} -r)\delta(\theta_{ij}-\theta)}{2\pi r^2 \sin(\theta)}\]

The angle \(\theta\) is defined with respect to a certain axis \(\vec{e}\) and is given by

\[\cos(\theta)=\frac{\vec{r}_{ij}\cdot\vec{e}}{r_{ij}e}\]

Here, we choose \(\vec{e}=\hat{e}_x\).

This version only works for 2D systems. For systems in 3D, the z coordinate is discarded.

References

[1] (1,2)

Bernard, E. P., & Krauth, W. (2011). Two-Step Melting in Two Dimensions: First-Order Liquid-Hexatic Transition. Physical Review Letters, 107(15), 155704. https://doi.org/10.1103/PhysRevLett.107.155704

[2]

Abraham, M. J., Hess, B., Spoel, D. van der, Lindahl, E., Apostolov, R., Berendsen, H. J. C., Buuren, A. van, Bjelkmar, P., Drunen, R. van, Feenstra, A., Fritsch, S., Groenhof, G., Junghans, C., Hub, J., Kasson, P., Kutzner, C., Lambeth, B., Larsson, P., Lemkul, J. A., … Maarten, W. (2018). GROMACS User Manual version 2018.3. www.gromacs.org

Parameters:

• coords (np.ndarray of shape (N,3)) – Particle coordinates.

• box_boundary (np.ndarray of shape (3,2)) – Boundary of the simulation box in the form of np.array([[xmin, xmax], [ymin, ymax], [zmin, zmax]]).

• other_coords (np.ndarray of shape (M,3), optional) – Coordinate frame of the other species to which the pair correlation is calculated. The default is None (uses coords).

• ndbins (int or None, optional) – Number of distance bins. The default is None.

• nabins (int or None, optional) – Number of angle bins. The default is None.

• rmax (float or None, optional) – Maximum distance to consider. The default is None.

• psi (np.ndarray of shape (2,) or None, optional) – Mean orientation of the whole system. If not None, the particles positions are rotated such that the x-axis of the system points into the direction of psi. According to Ref. [1], use \(\psi=(Re(\Psi_6),Im(\Psi_6))\), where \(\Psi_6\) is the mean hexagonal order parameter of the whole system. The default is None.

• njobs (int, optional) –

  Number of jobs used for parallel computing.The default is 1. Rule of thumb: Check how many your system has available with

  >>> import os
  >>> os.cpu_count()
  

  and set njobs to between 1x this number and 2x this number.

• pbc (bool, optional) – If True, periodic boundary conditions are applied. The default is True.

• verbose (bool, optional) – If True, a progress bar is shown. The default is False.

• chunksize (int or None, optional) – Divide calculation into chunks of this size. The default is None.

Returns:

• gr (np.ndarray) – \(g(r,\theta)\) (2D array of floats)

• R (np.ndarray) – distances (meshgrid)

• T (np.ndarry) – Angles (meshgrid)

Examples

>>> import amep
>>> import numpy as np
>>> traj = amep.load.traj("../examples/data/lammps.h5amep")
>>> frame = traj[-1]
>>> grt, rt, theta = amep.spatialcor.pcf_angle(
...     frame.coords(), frame.box, njobs=4,
...     ndbins=1000, nabins=1000
... )
>>> X = rt*np.cos(theta)
>>> Y = rt*np.sin(theta)
>>> fig, axs = amep.plot.new(figsize=(3.8,3))
>>> mp = amep.plot.field(axs, grt.T, X, Y)
>>> cax = amep.plot.add_colorbar(
...     fig, axs, mp, label=r'$g(\Delta x, \Delta y)$'
... )
>>> axs.set_xlim(-10,10)
>>> axs.set_ylim(-10,10)
>>> axs.set_xlabel(r'$\Delta x$')
>>> axs.set_ylabel(r'$\Delta y$')
>>> fig.savefig('./figures/spatialcor/spatialcor-pcf_angle.png')
>>>